In Part 1, we created the parameters for a circuit that can verify that a triple $(a, b, c)$ is a Pythagorean triple. In Part 2 we created a proof for an assignment to the circuit using $(3,4,5)$. In this part of PLONK by Hand we will verify the proof from Part 2.

We will do some elliptic curve arithmetic, so the table of elliptic curve points from Part 1 will be handy to have around. Once the elliptic curve arithmetic is finished we will use the results to compute two elliptic curve pairings and check that the pairing values are equal. The pairings are computed with some techniques and optimizations from the excellent Pairings for Beginners by Craig Costello.

Verifier Preprocessing

Some information about a circuit and its inputs is public, and the Verifier will need to use this information to verify the proof. The selector polynomials $q_M$, $q_L$, $q_R$, $q_O$, and $q_C$ as well as the permutation polynomials $S_{\sigma_1}$, $S_{\sigma_2}$, and $S_{\sigma_3}$ describe the circuit and are publicly known. The Verifier uses the SRS to evaluate these polynomials at the secret number $s$.

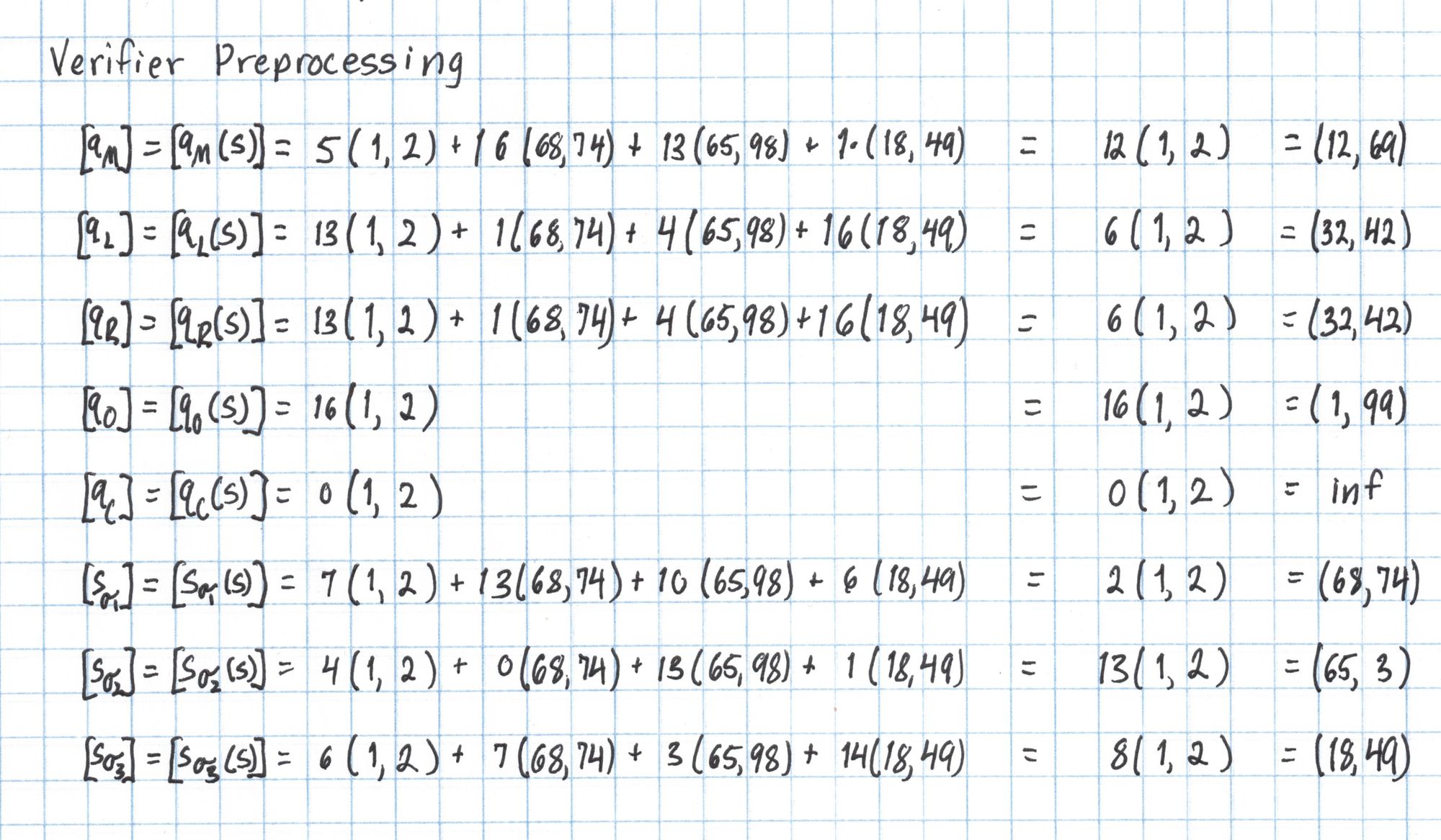
One More Roll

Before we begin, the Verifier needs a random evaluation point $u$.

The Verifier algorithm

The Verifier arithmetically combines the proof and any public information and checks that a single equation holds. If using Kate polynomial commitments this equation will involve evaluating an elliptic curve pairing.

Here's the whole verifier algorithm written out:

First we verify that the elliptic curve points are actually on the curve $E$ we constructed in Part 1. (That curve was $E:y^2=x^3+3$ over the field $\mathbb{F}_{101}$.)

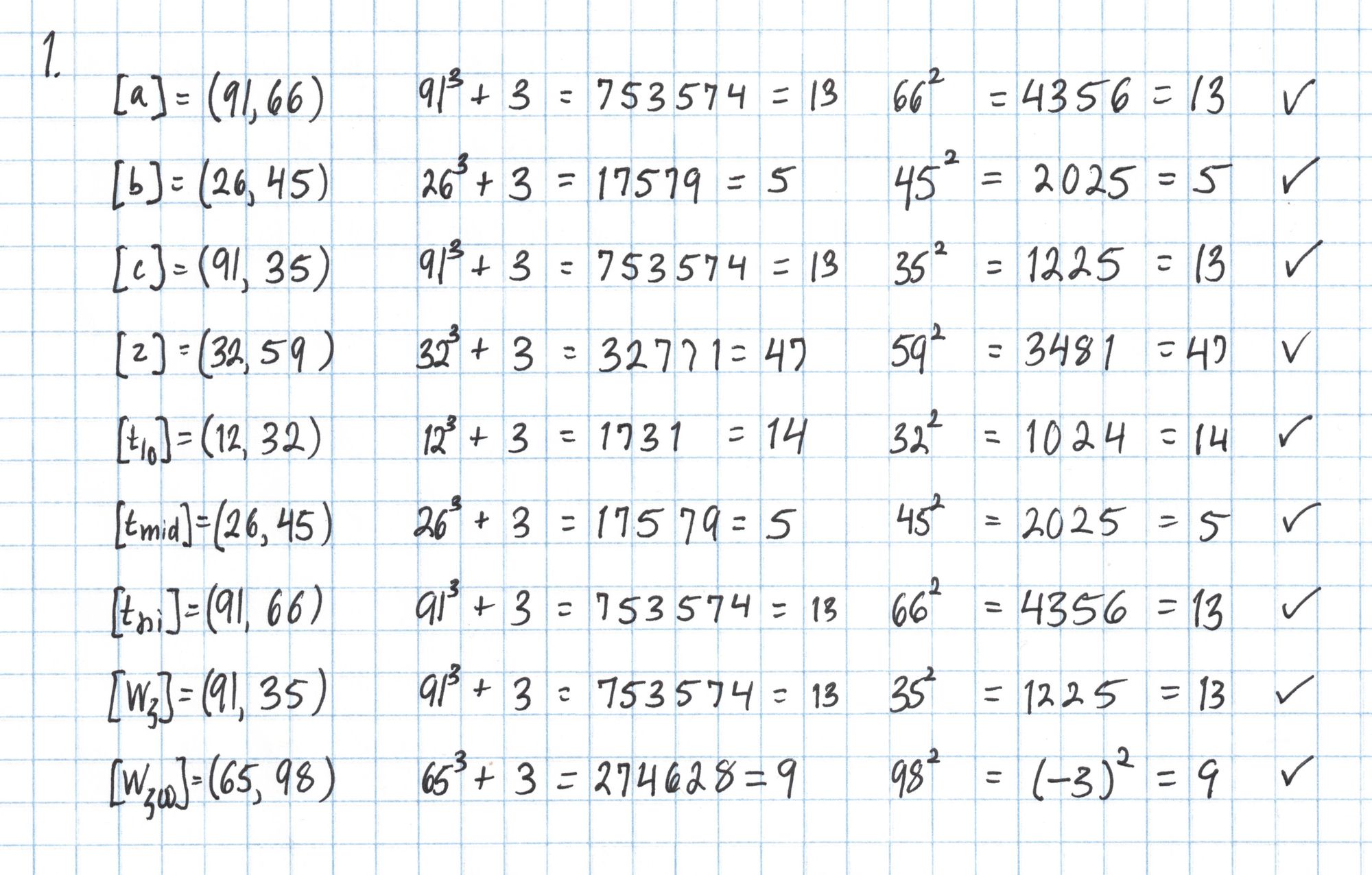
Then we make sure the field elements in the proof are in $\mathbb{F}_{17}$, which just amounts to checking that each integer is less than 17.

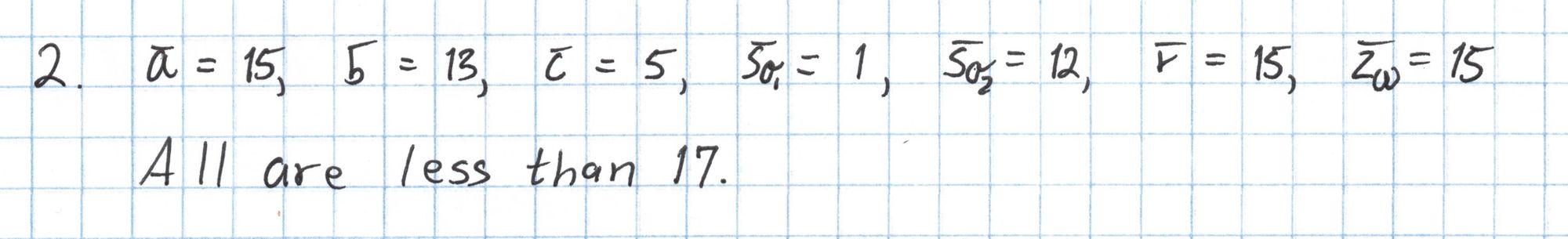
The next several steps build up the components we will use in the final pairing check. Our Pythagorean circuit doesn't have any public inputs, so we can skip Step 3. Then we evaluate the zero polynomial $Z_H$ at $\mathfrak{z}=5$.

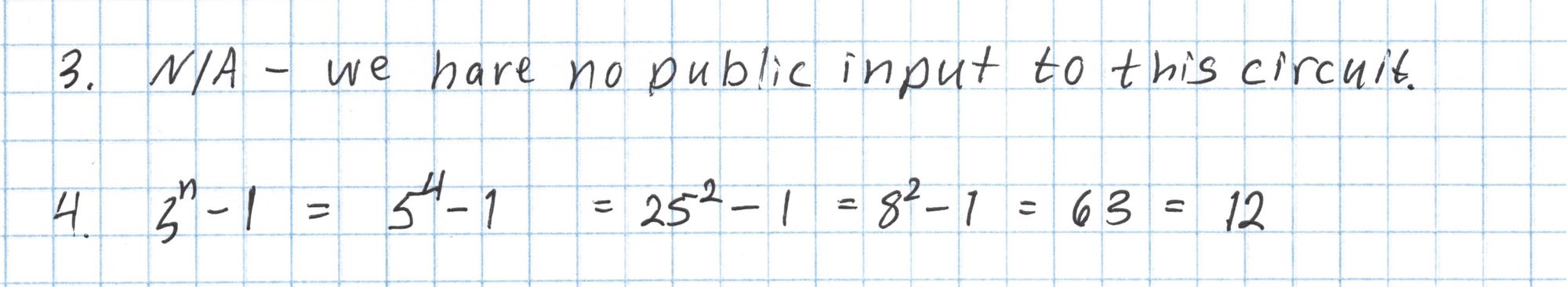
We continue building up the components that will go in to the final pairing check.

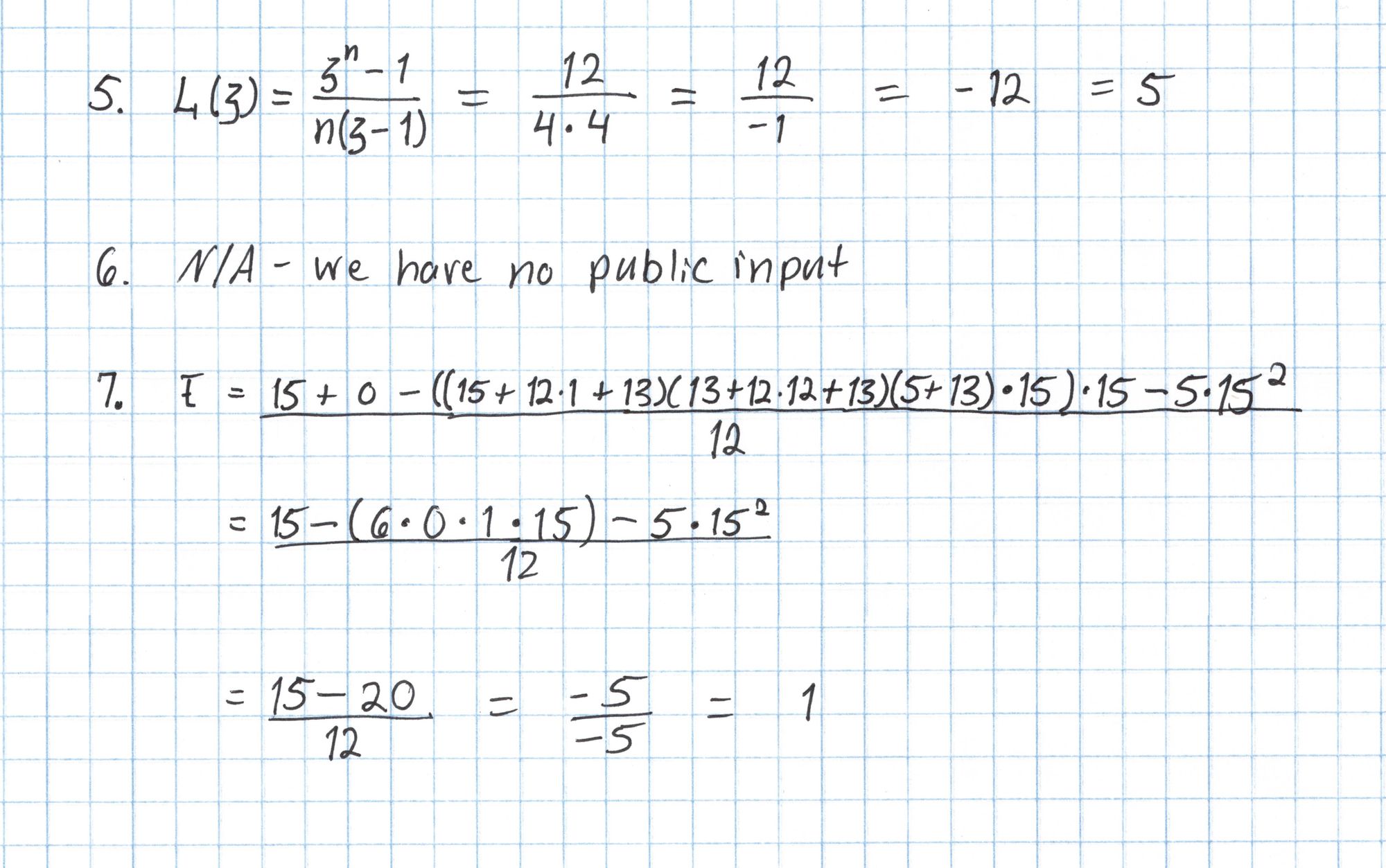
The last few computations are done with elliptic curve points. In practice this elliptic curve arithmetic would use very large scalars and would be done with a double-and-add style algorithm making the computations feasible. In our case, we have a small table of elliptic curve points from Part 1 that let us cheat and avoid much of this arithmetic.

The points $[D]$, $[F]$, and $[E]$ are closely related to the batched polynomials $W_\mathfrak{z}$ and $W_{\mathfrak{z}\omega}$ from Round 5 of the Prover's protocol, except that the formulas for computing these points incorporate the new random evaluation point $u$.

The point $[F]$ is a commitment to a polynomial $W_\mathfrak{z} + uW_{\mathfrak{z}\omega}$ at the secret number $s$ and the point $[E]$ is an opening of the same polynomial at $\mathfrak{z}$.

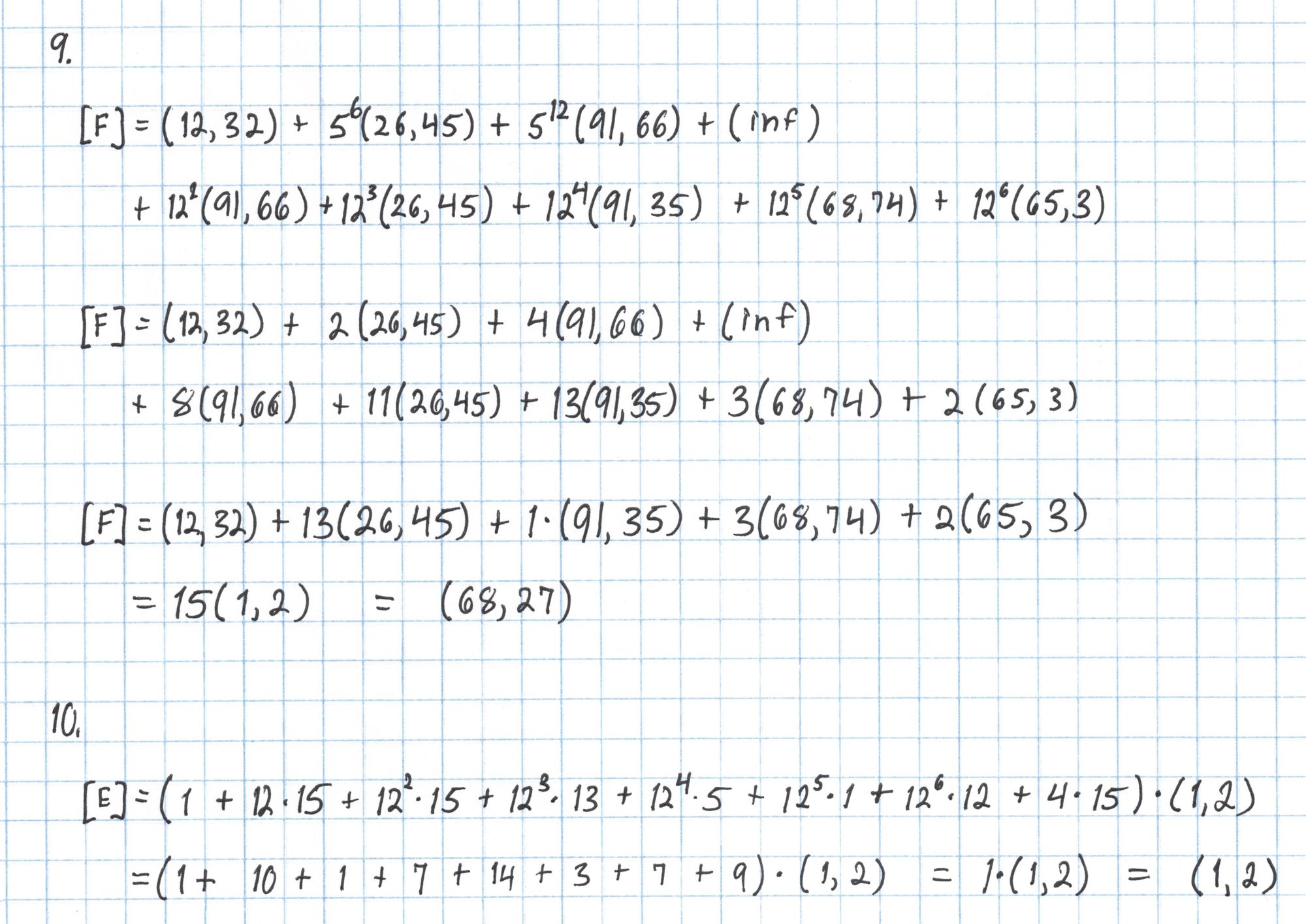
Now we construct the final pairing equation.

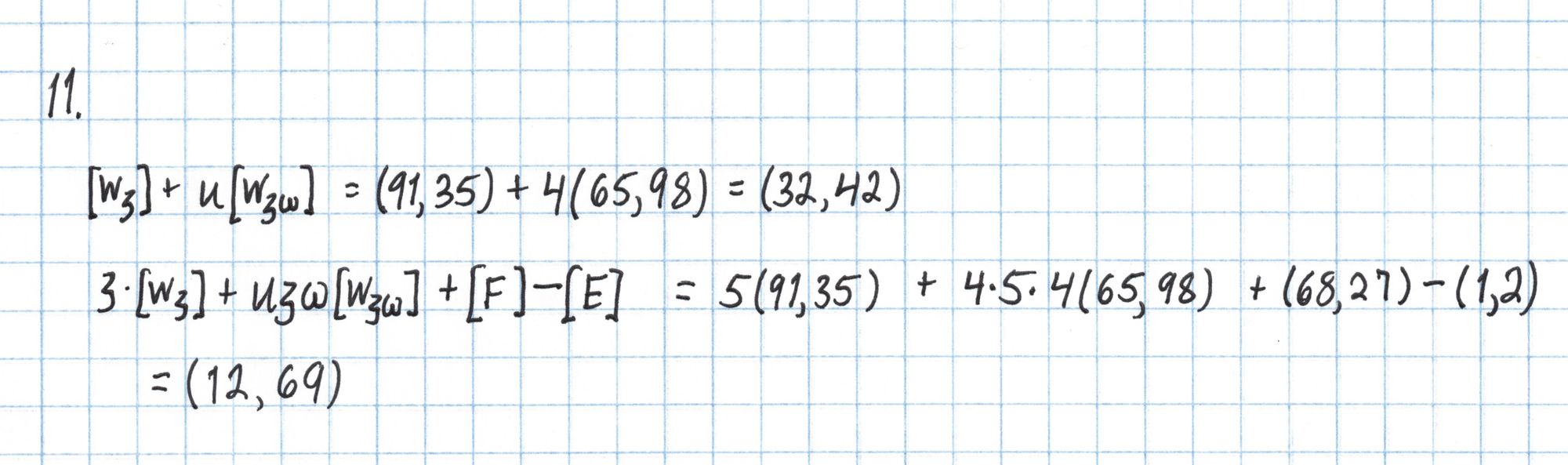
All that remains is to compute the pairings on each side of this equation.

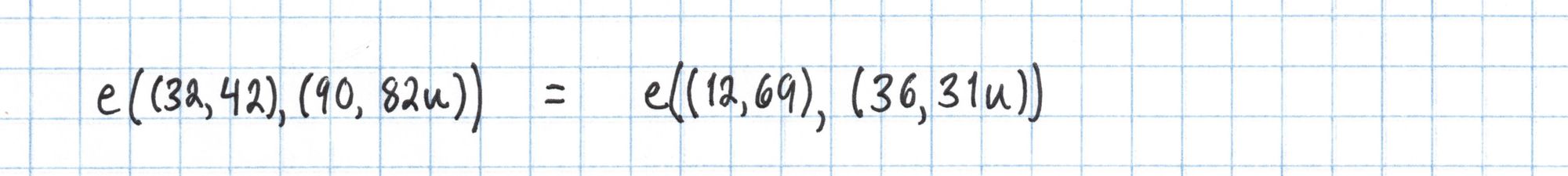
The Pairing

To compute a pairing of two elliptic curve points, we use a Miller loop process to create a polynomial function in $x$ and $y$. This function is created using one of the two points being paired. We then evaluate the function at the $x$ and $y$ coordinates of the second point.

In order to save some time we'll use the bilinearity of the pairing to rewrite each side of the equation to use the same point as the basis for the Miller loop. This will let us reuse some of our work. Again, this is only possible beacause of our "cheat" table from Part 1.

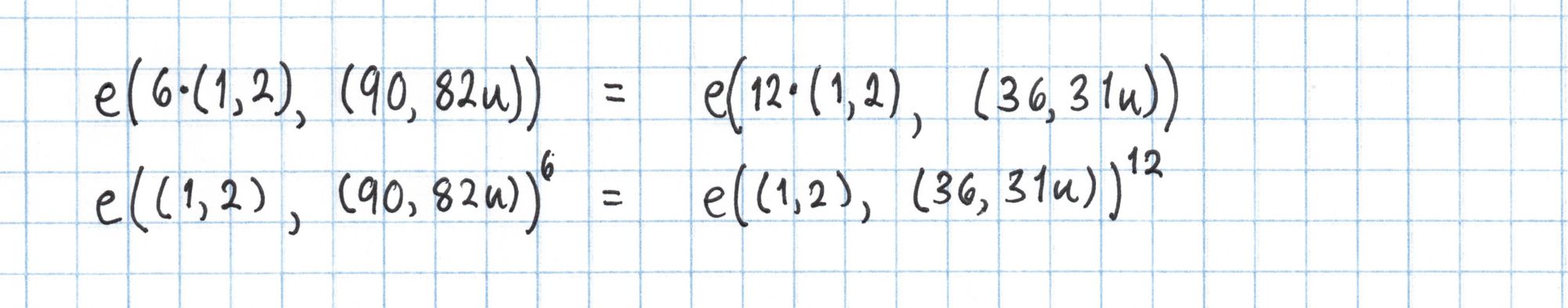
Here is a simplified definition for the pairing $e$. This definition takes into account several optimizations and leaves out some details that happen to not affect our result. See Pairings for Beginners by Craig Costello for a more general definition.

Since our $r=17$ we will construct a function $f_{17}$ using a double-and-add style algorithm starting with $f_1$. We will "double" four times to get $f_{16}$ and "add" once to get $f_{17}$. We need to compute lines through $P$ and $-2P$, $2P$ and $-4P$, $4P$ and $-8P$, $8P$ and $-16P$, and finally $16P$ and $P$. We'll precompute these line functions to save us some work later.

Computing these lines is pretty simple. We just use the normal process for getting the equation of a line from two points. The first two are done here:

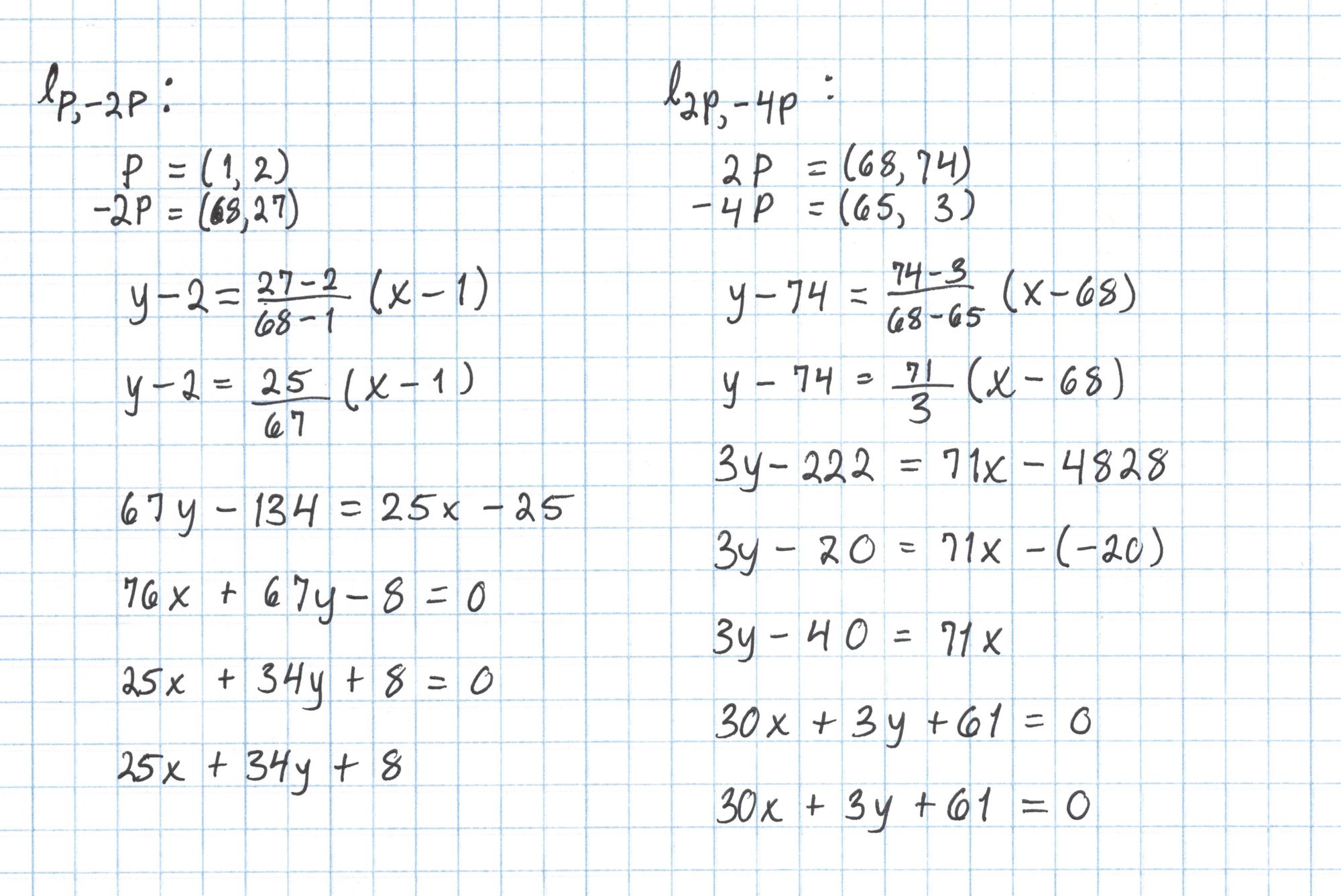
Here is the full list of lines we'll need. Since $16P$ = $-P$ the last line is just the vertical line through $P$.

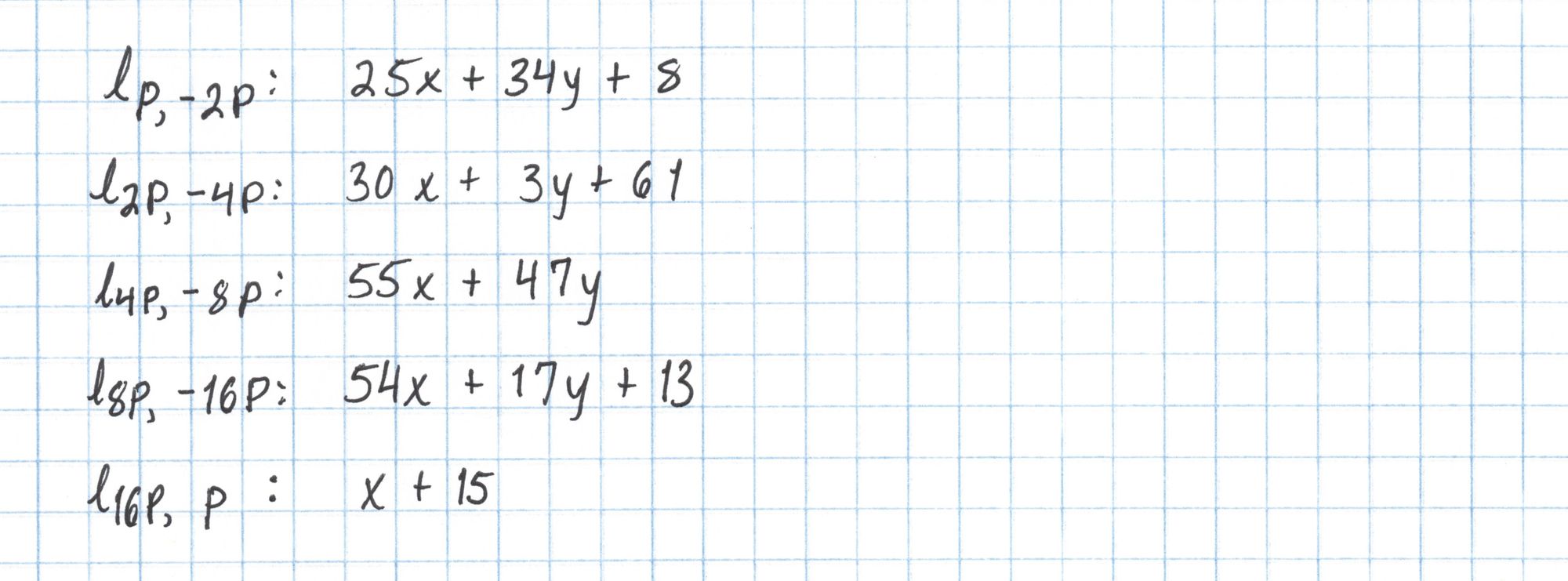
Now that we have precomputed these lines we can evaluate the pairing. Rather than creating a large degree-16 polynomial, we will compute the evaluation in steps. In each step we evaluate a linear factor using the coordinates of the second point in the pairing. The result is then included in the next calcuation. This procedure is the Miller loop.

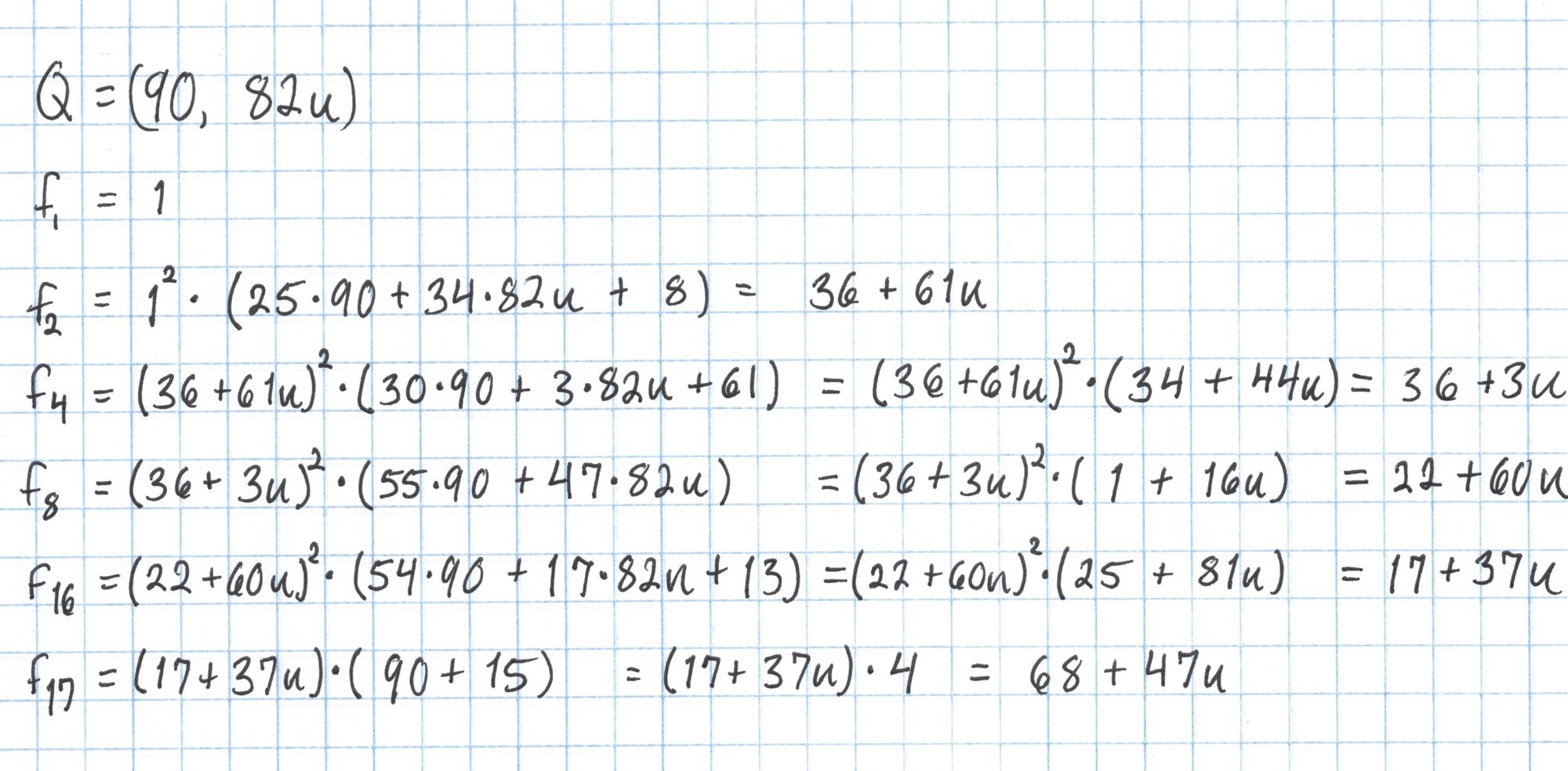
We aren't done yet, since we need to raise this result to the $(p^k-1)/r$ power. This is called the "final exponentiation" and can be an expensive part of the pairing computation.

Our exponent is $(101^2-1)/17 = 600$. We could use a square-and-multiply method to do this in about 13 steps, which, considering some of the calculations we have done in this series isn't totally unreasonable.

However, there is a shortcut using the Frobenius map. Raising an element of an extension field $\mathbb{F}_{p^k}$ to the power $p$ will return a conjugate of that element. For us this means $(a+bu)^{101} = a-bu$. Here's how we can use this to our advantage to perform our exponentiation in a lot fewer steps:

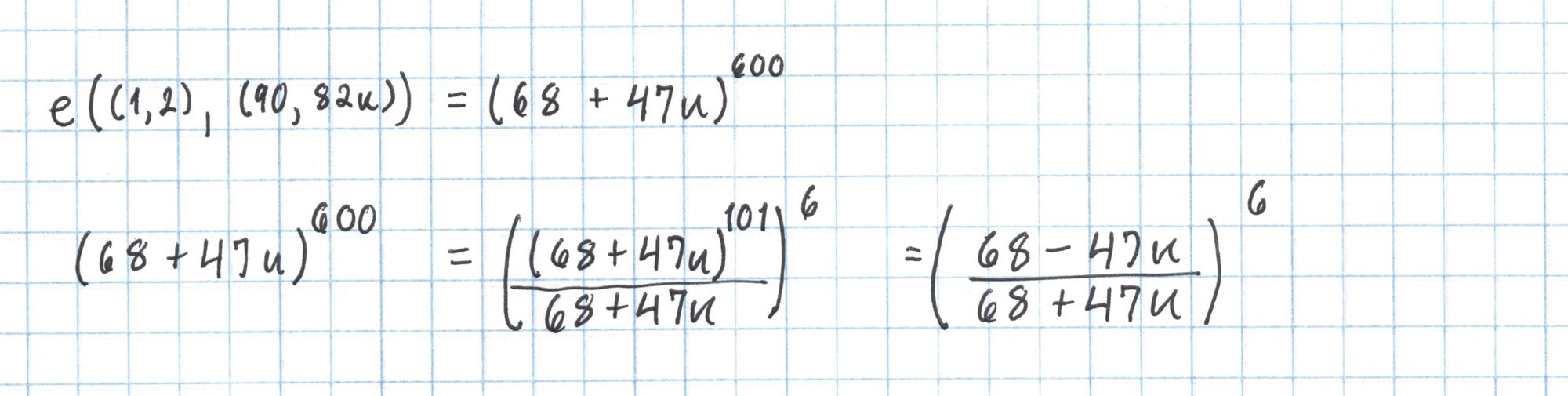
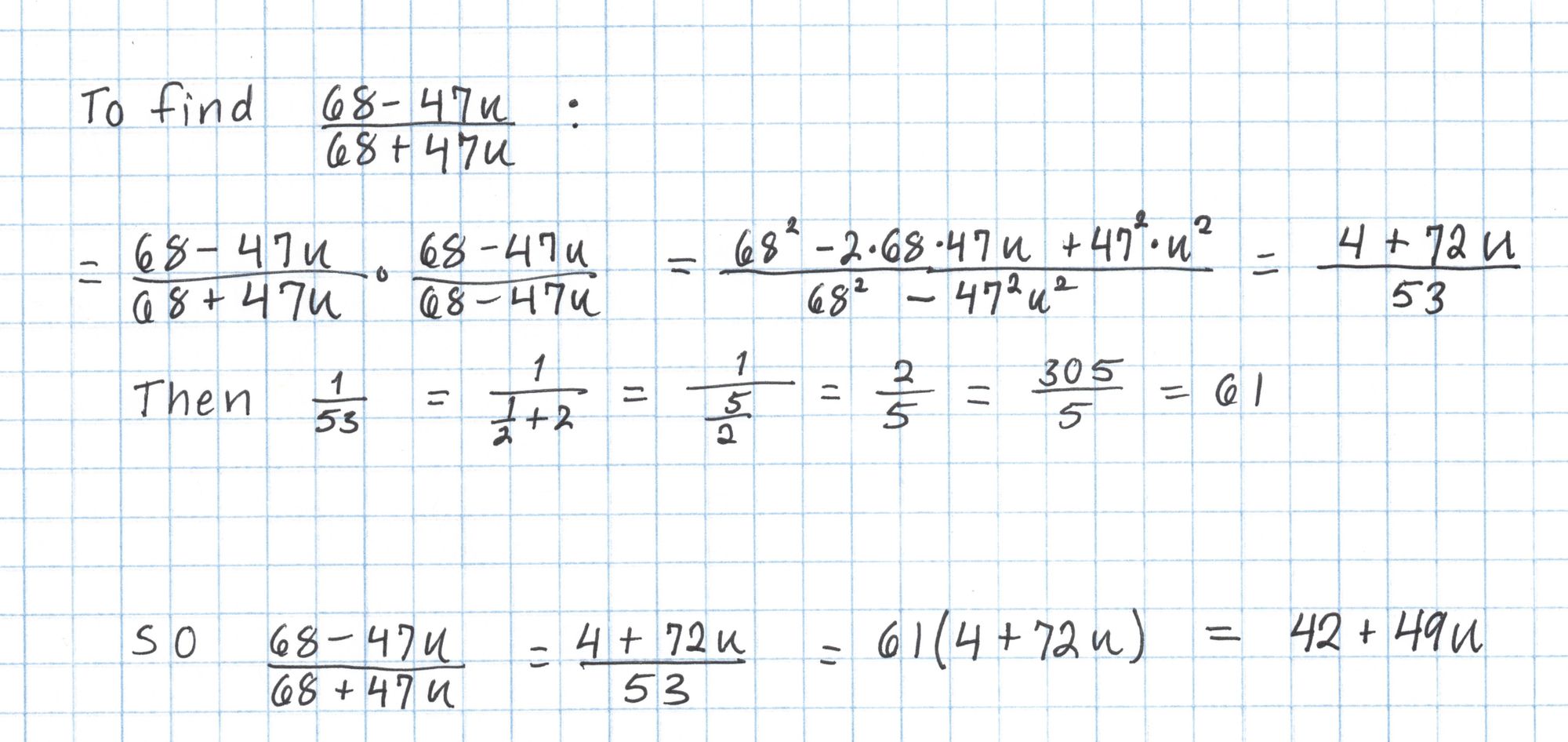
Finally we take $42+49u$ to the sixth power.

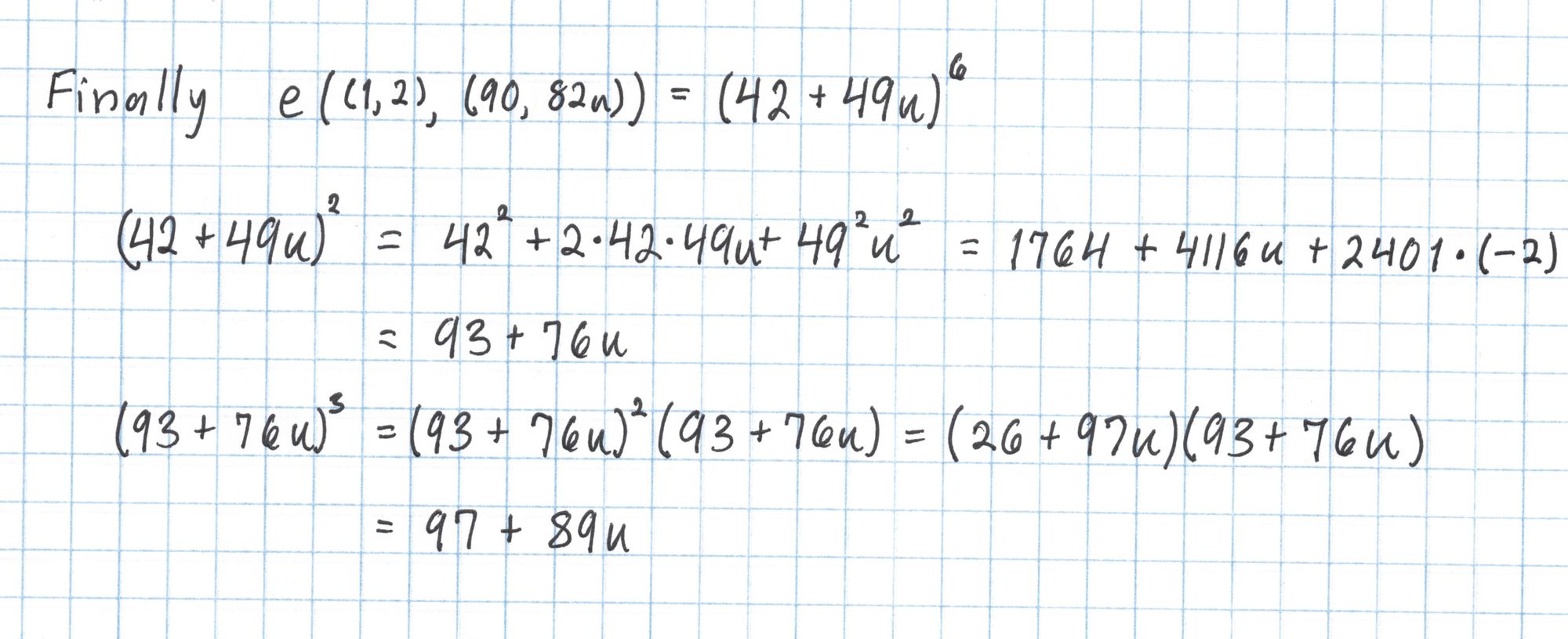
We repeat the same process with $Q=(36, 31u)$ to calculate the right side of the pairing equation.

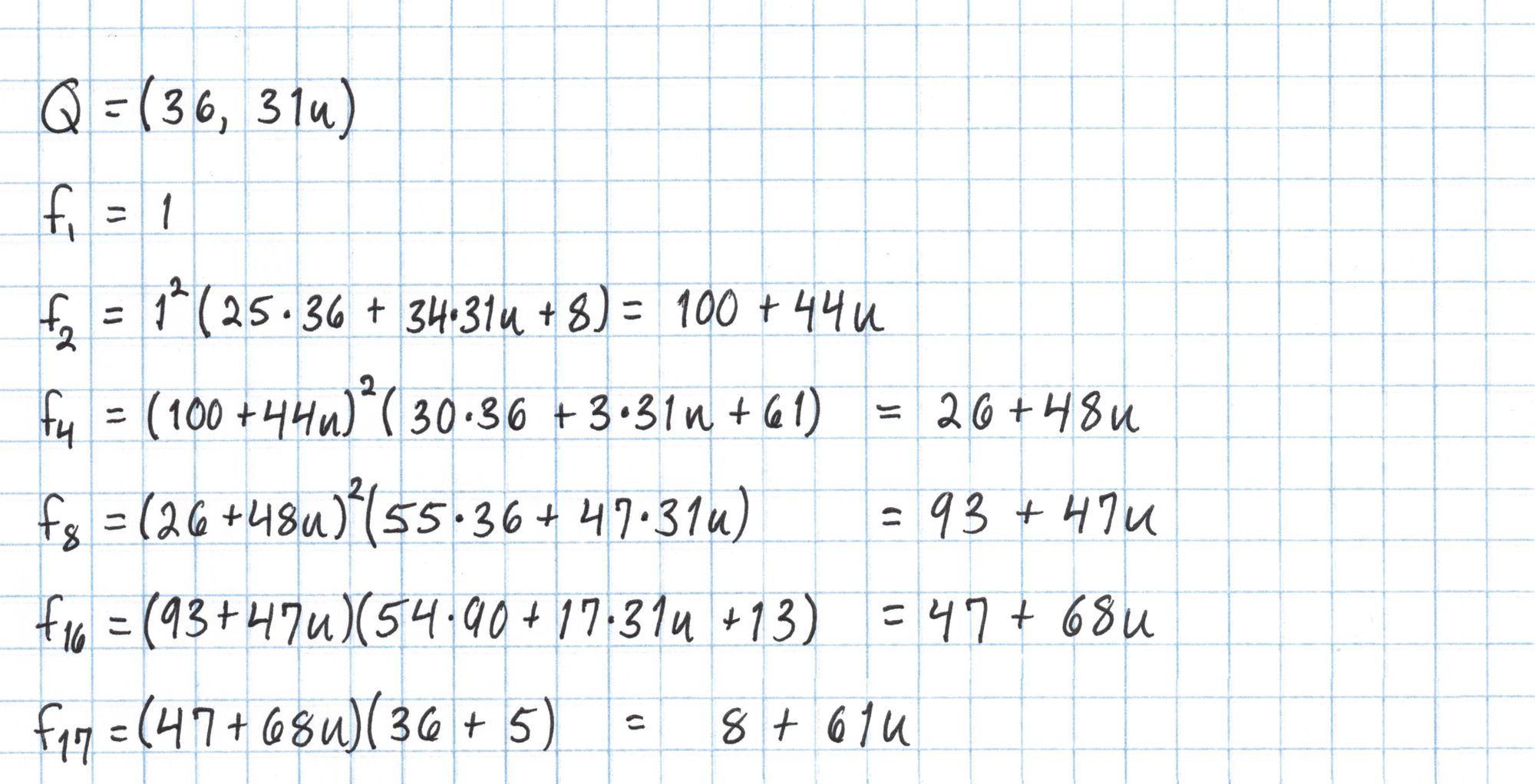
Then we'll use the same Frobenius trick for the final exponentiation.

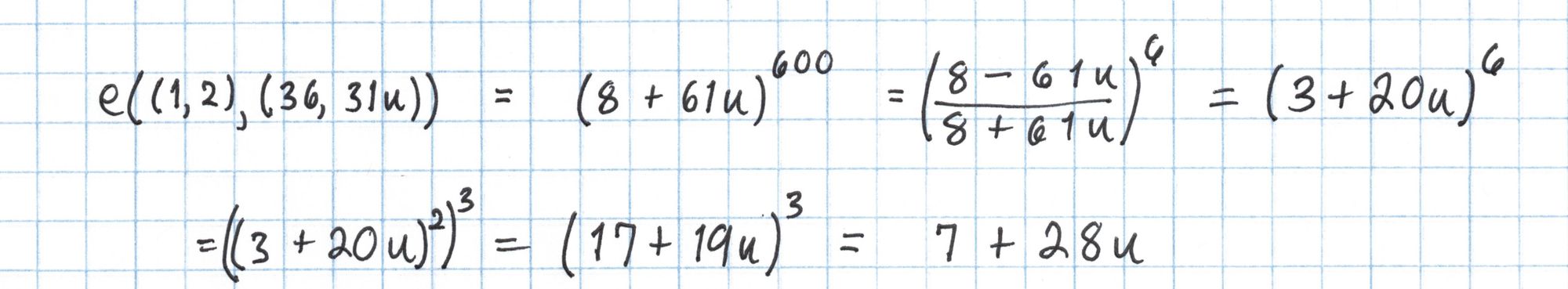
Now we're ready to check the pairing equation.

The proof is accepted!

Written by Joshua Fitzgerald, zero-knowledge cryptography researcher & protocol developer at Metastate.

Image credits: Koala, Birdland Animal Park, Batemans Bay NSW from Wikimedia.

Metastate has ceased its activities on the 31st of January 2021. The team members have joined a new company and working on a new project. If you're interested in zero-knowledge cryptography and cutting-edge cryptographic protocols engineering positions in Rust, check out the open positions at Heliax.

If you have any feedback or questions on this article, please do not hesitate to contact us: hello@heliax.dev.