Introduction
In this series of posts, we will show how to execute a PLONK zero-knowledge proof system completely by hand. All of the math used in these posts can reasonably be done with just pencil-and-paper (and a little patience). For each kind of computation we will give you at least one fully worked example—often several—and tricks to help save time and notebook paper.
Most of the math we will do is elementary, though some higher-level concepts do appear. This series assumes the reader is familiar with polynomial and matrix arithmetic as well as finite fields and their simple extensions.
Having some knowledge about elliptic curves will be helpful, but the needed formulas are provided and can be used even if you are unfamiliar with them.
While this series is intended to show that even a complex construction like PLONK can be done on paper, you might want to use a computational helper like WolframAlpha to move through the posts more quickly, if you wish.
In this first post we will show you how to choose parameters, run a trusted setup, and convert a statement into a PLONK-style circuit by hand. The next post will show you how to create a proof, and in the final post in the series we will verify the proof.
PLONK
PLONK is a recent zk-SNARK construction that can do much more than older SNARKs. If combined with Kate polynomial commitments it becomes a universal SNARK, meaning the reference string created in a trusted setup can be re-used for any other PLONK circuit of the same size (or less) than the original. The reference string can also be updated, with each update reducing the chance that the setup was compromised by collusion. Other polynomial commitment schemes can turn PLONK into a kind of STARK with no trusted setup at all.
Parameters
PLONK needs some kind of polynomial commitment scheme, and we will use Kate commitments here. Kate commitments require an elliptic curve on which we can compute an elliptic curve pairing. Usually we would pick BN-254, BLS12-381, or some other well-known pairing-friendly curve. (An elliptic curve is considered "pairing-friendly" if its pairing function is efficiently computable without sacrificing security.) We will use a curve that isn't very pairing-friendly so that we can get a pairing function that is much easier to compute by hand (although it will be very insecure). For more on elliptic curve pairings, check out this excellent blog post from Vitalik Buterin or this one from Joshua Fitzgerald.
An elliptic curve is an equation of the form $y^2=x^3+ax+b$, where $a$, $b$, $x$, and $y$ are elements of some field. (In a cryptographic setting the field will be a finite field.) Any $(x,y)$ pairs satisfying the equation are points on the curve.
We will use an elliptic curve over the field $\mathbb{F}_{101}$, which makes hand computation easy. This field has a lot of handy substitutions that we will make use of often: $100 \equiv -1$, $50 \equiv -\frac{1}{2}$, $20 \equiv -\frac{1}{5}$, and so on.
The elliptic curve $y^2 = x^3 +3$ is a commonly-used elliptic curve equation, and $(1,2)$ is an easy-to-find point on that curve we can use as a generator. In fact, the alt_bn128 curve that is implemented on Ethereum uses this same curve equation and generator, but over a much larger field.
Points on elliptic curves form a "group" meaning two points can be "added" in some way to get another point on the curve. We can "double" a point by adding it to itself, or invert a point to find its additive inverse. Here are the formulas for doubling and inverting an elliptic curve point on our curve:
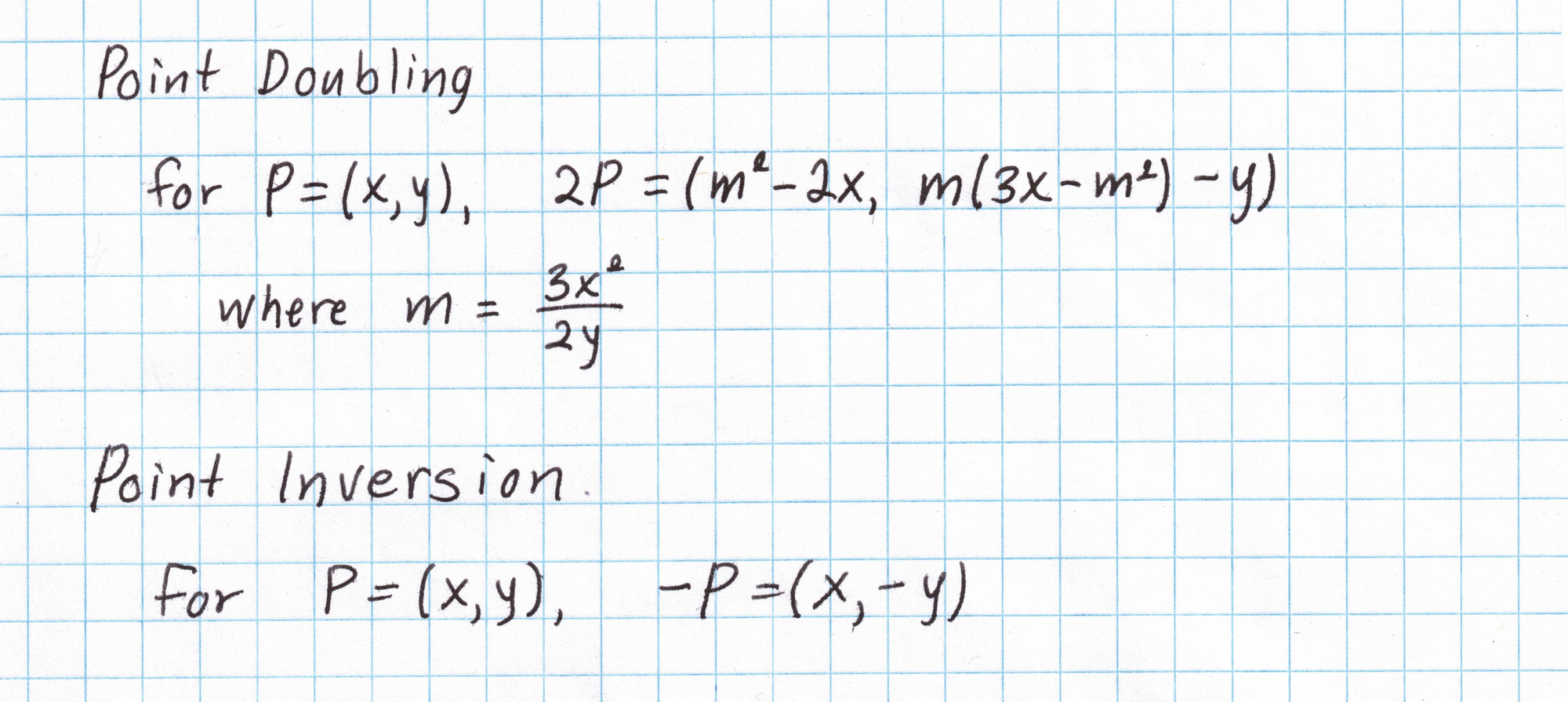
Elliptic curves also have an abstract "point at infinity" which serves as the group identity. For more on elliptic curve arithmetic, check out this post from Nick Sullivan.
It will be nice to have a table of multiples of this generator to save some work later on. (This is only practical on elliptic curves of small order, like ours.) Taking the generator $G_1 = (1,2)$ and applying the doubling formula gives us $2G_1$, then the inversion formula gives us $-2G_1$. We can double again to get $4G_1$ and $-4G_1$, and so on. Each doubling requires a fair amount of arithmetic in the field $\mathbb{F}_{101}$. After just a few doublings we can see that the subgroup generated by $(1,2)$ has order 17.
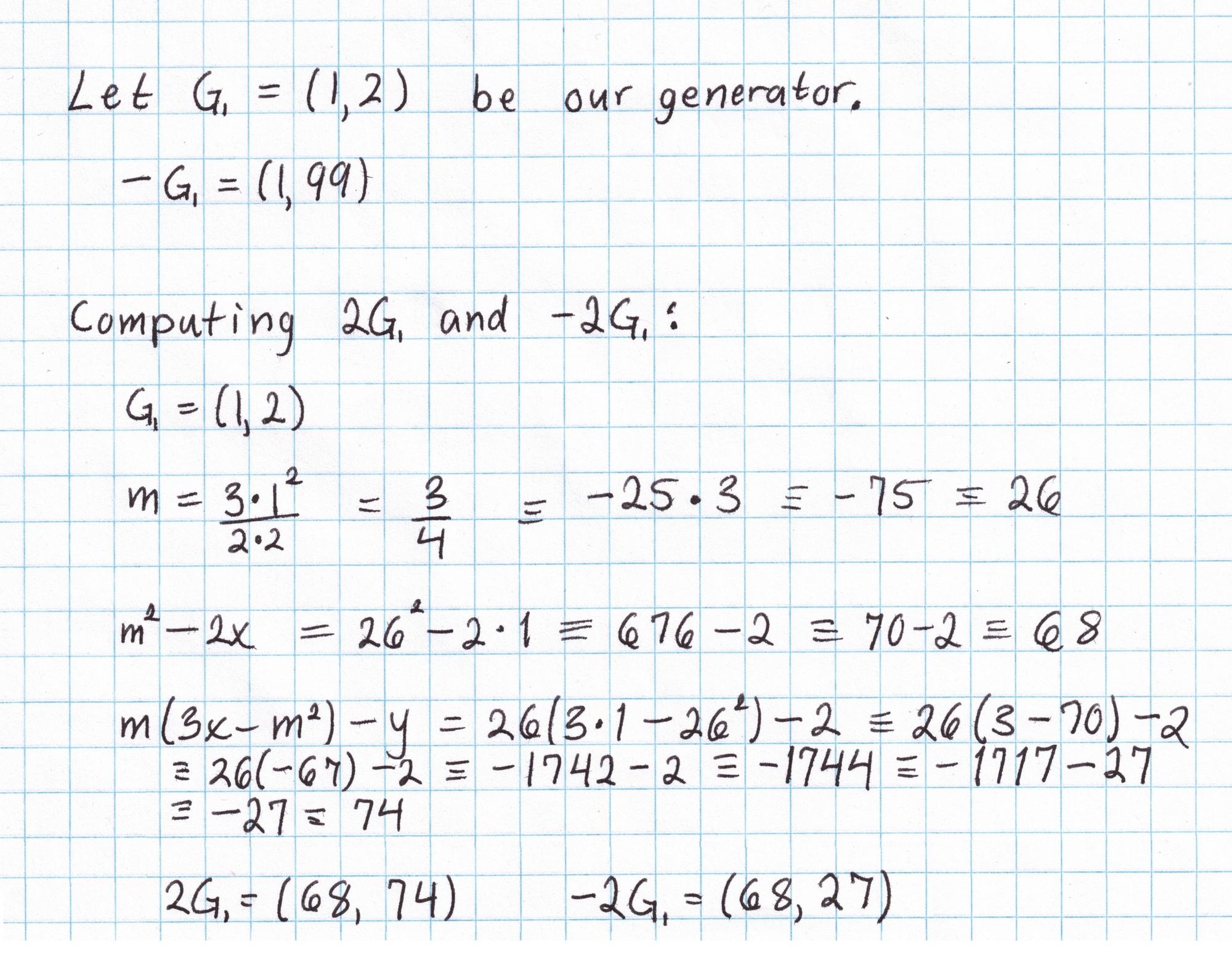
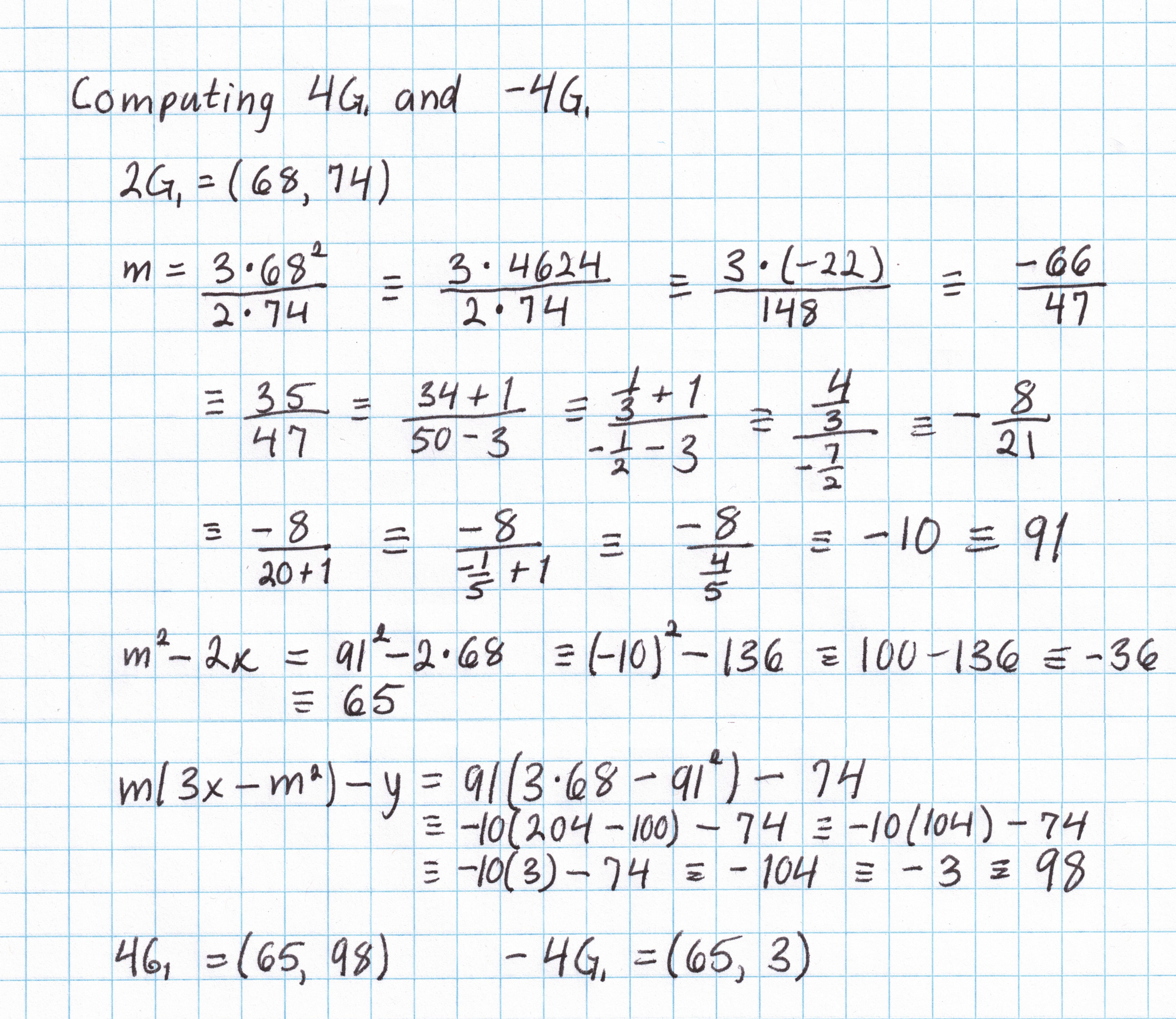
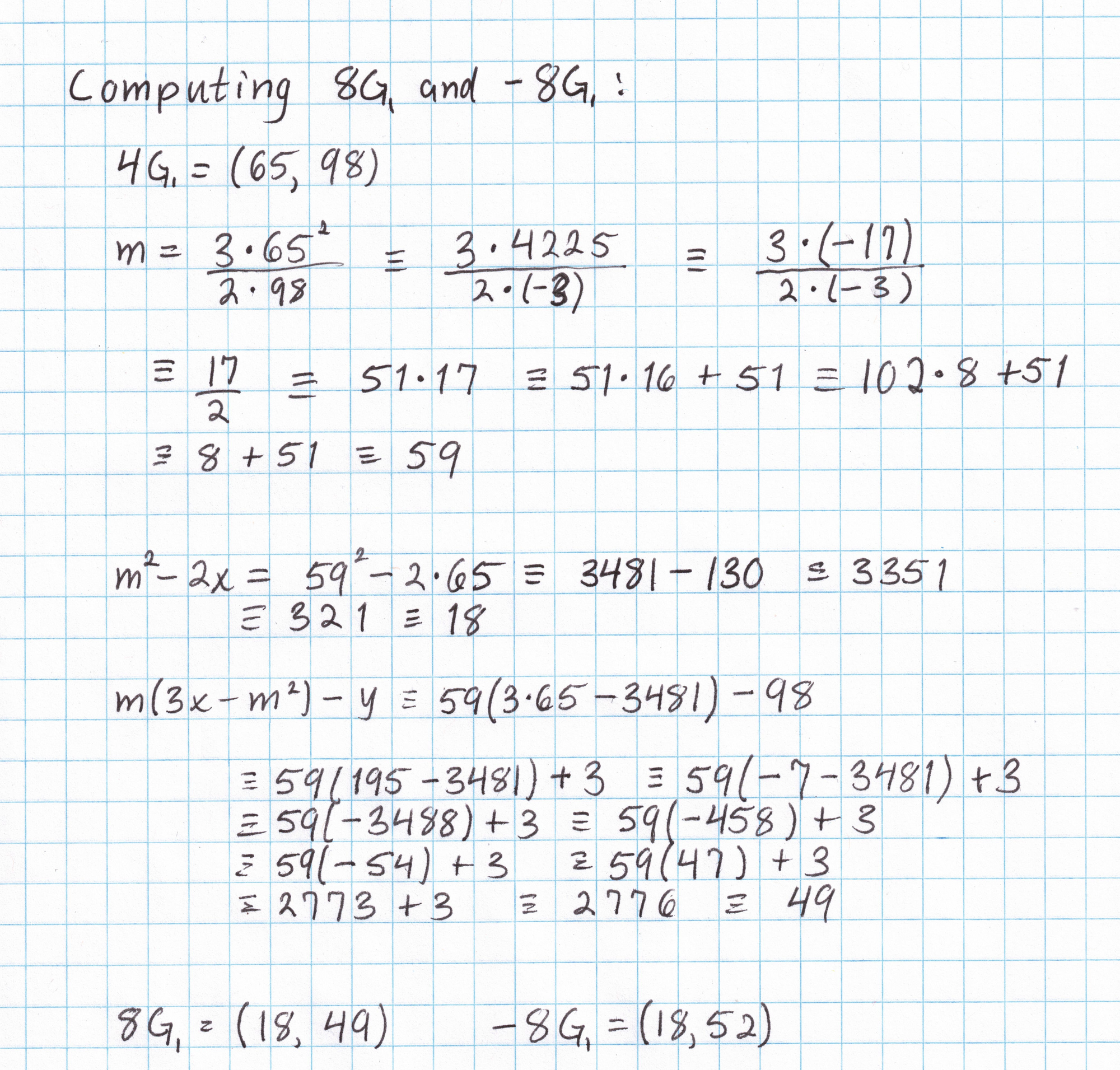
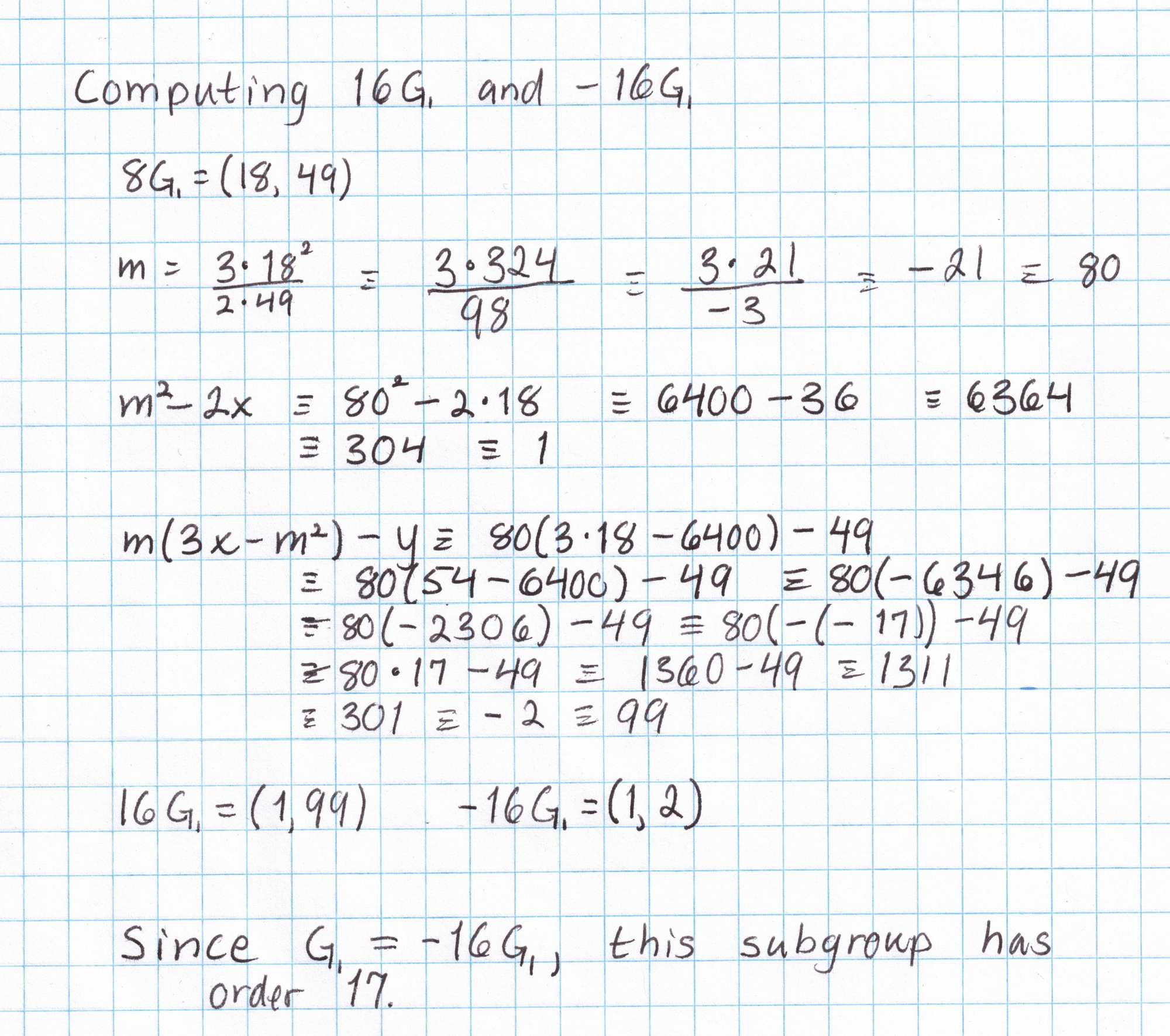
By the time we've done a few doublings, we already know a majority of the points in this subgroup. A few more additions (like $G_1$ + $2G_1$ to get $3G_1$) are all that is needed to get a complete picture of this subgroup. (I've omitted the work needed to get the rest of the points. If you want to do this yourself you'll need the elliptic curve addition formula.)

Making a list of all the multiples of an elliptic curve point is only feasible if the order of that point is small. Generators on elliptic curves used in practice are far too large to make an exhaustive list like this, which is a good thing, since having this table allows us to break any cryptography that uses this curve on this field.
Preparing for Pairings
Now that we have a suitable elliptic curve subgroup, we will need to do some further work to enable us to compute an elliptic curve pairing later on. The excellent Pairings for Beginners by Craig Costello was the source for much of the following work.
Embedding Degree
We found an elliptic curve subgroup of order 17 where the coordinates of the points come from $\mathbb{F}_{101}$ and satisfy $y^2=x^3+3$. However there are more points "out there" that satisfy this relationship. Some may have coordinates from an extension field $F_{101^k}$. It's natural to ask how many other points of order 17 we can expect to be out there, and what is the highest degree extension field we will need to use for coordinates in order to find them?
The degree of the extension field of characteristic $p$ that contains every point of order $r$ on the elliptic curve is the embedding degree. It has a simple formula: the embedding degree is the smallest number $k$ such that $r|p^k-1$.
It turns out that the embedding degree for our curve using $r=17$ is $2$. (Higher embedding degrees would be more secure, but harder to compute with. As usual, for this post we are sacrificing security for ease of computation.) All of the elliptic curve points of order 17 can be found using coordinates from $\mathbb{F}_{101^2}$.
How many other points with order 17 are there, in total? A wonderful result says that if $r$ is relatively prime to the charactersitc $p$ of the field, then there will be exactly $r^2$ points of order $r$ in $\mathbb{F}_{p^k}$.
The Extension Field
The extension field $\mathbb{F}_{101^2}$ can be generated from $F_{101}$ by adjoining a solution to a degree-2 polynomial that is not found in $F_{101}$. The polynomial $x^2+1$ splits in $F_{101}$ as $(x+10)(x-10)$ and so isn't suitable. However $x^2+2$ is irreducible in $F_{101}$ and can be used to generate the extension. Let $u$ be one of the solutions to $x^2+2$. Now every element of $F_{101^2}$ can be written as $a+bu$, where $a$ and $b$ are from $F_{101}$.
Subgroup 2
We will be computing an elliptic curve pairing later on in this series in order to check our Kate polynomial commitments. Elliptic curve pairings take a pair of points on an elliptic curve which have the same order and return an element of the field $\mathbb{F}_{p^k}$. One complication when working with pairings is that the two elliptic curve points must come from different elliptic curve subgroups that have the same order. So in addition to the subgroup we just computed above we will need to find a generator for a second subgroup that also has order 17.
There are a few different techniques for finding a second subgroup. Because our embedding degree is $2$, there must be some points of order 17 with coordinates in $\mathbb{F}_{101^2}$. Since 17 is prime, if we can find just one of them we can be sure that it is a generator of the second subgroup. A suitable generator is $(36, 31u)$, which was found following the twisted curve technique from Pairings for Beginners. Remembering that $u^2 = -2$ we can easily verify this is a point on our curve by checking that $y^2=x^3+3$ in $\mathbb{F}_{101^2}$.
Running the Trusted Setup
Kate commitments require a trusted setup ceremony where a structured reference string (SRS) is created and the "toxic waste" is discarded.
The reference string is a list of elliptic curve points parameterized by a randomly-generated secret number $s$, which is part of the toxic waste. Any circuit can use any similar SRS as long as it has enough elements. According to the PLONK protocol paper, a circuit with $n$ gates requires an SRS with at least $n+5$ elements as below:
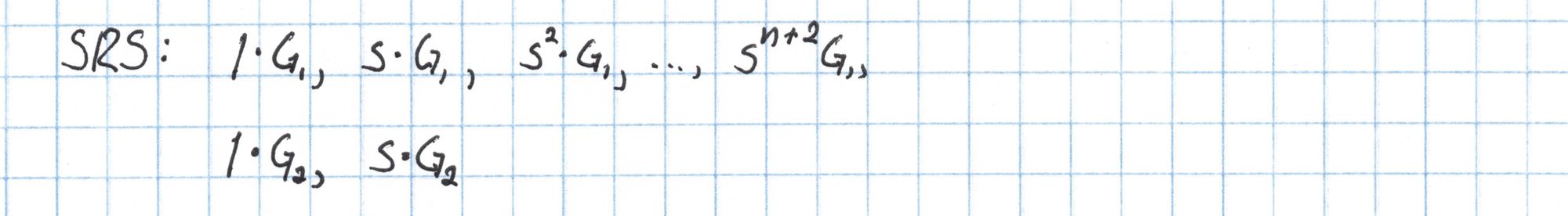
The elliptic curve points $G_1$ and $G_2$ are the generators of the two subgroups we intend to use in our pairing.
We can use something random to generate $s$. Since the number $s$ is a coefficient multiplying the generator from our elliptic curve group, it needs to be less than the order of the group (17). A 20-sided die works pretty well for this, though we'd need to re-roll if we rolled a 1 or something higher than 16.
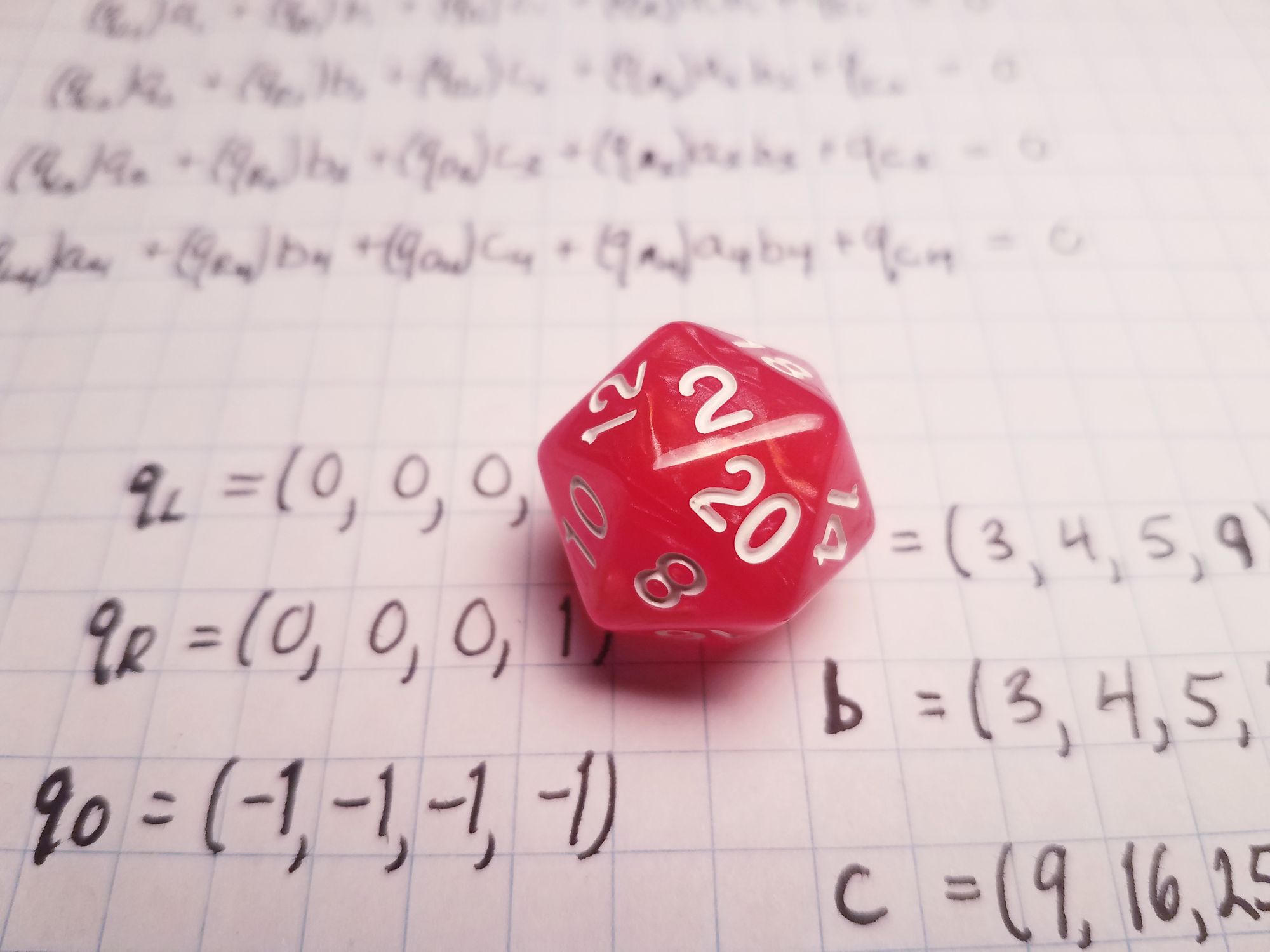
Using this random number we create the structured reference string. Our SRS will have 9 elements (since I know the circuit we'll be using later will have 4 gates). First we can find the powers of $s$ that will serve as coefficients for our two generators.
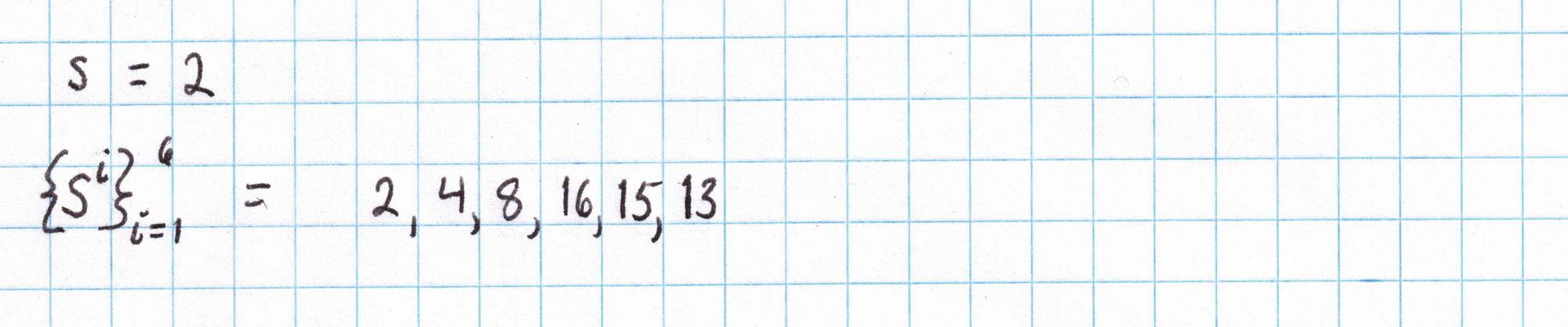
Then we will use our table of elliptic curve points to construct the first part of the SRS with generator $G_1$. Normally this would be much lengthier process, but we benefit from having a very small $s$ and cheat table for our elliptic curve.
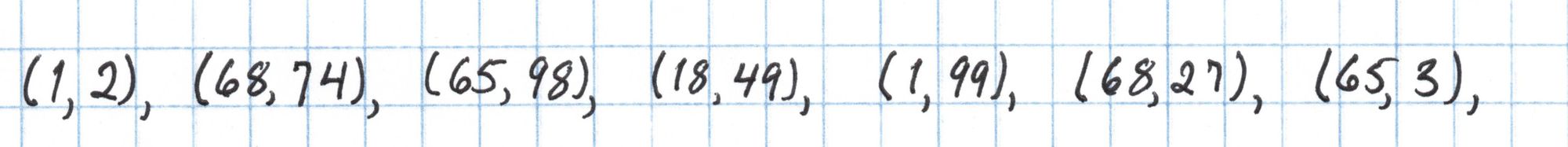
For the second line of the SRS we only need to compute $2G_2$. We can do this using the exact same doubling formula from earlier.
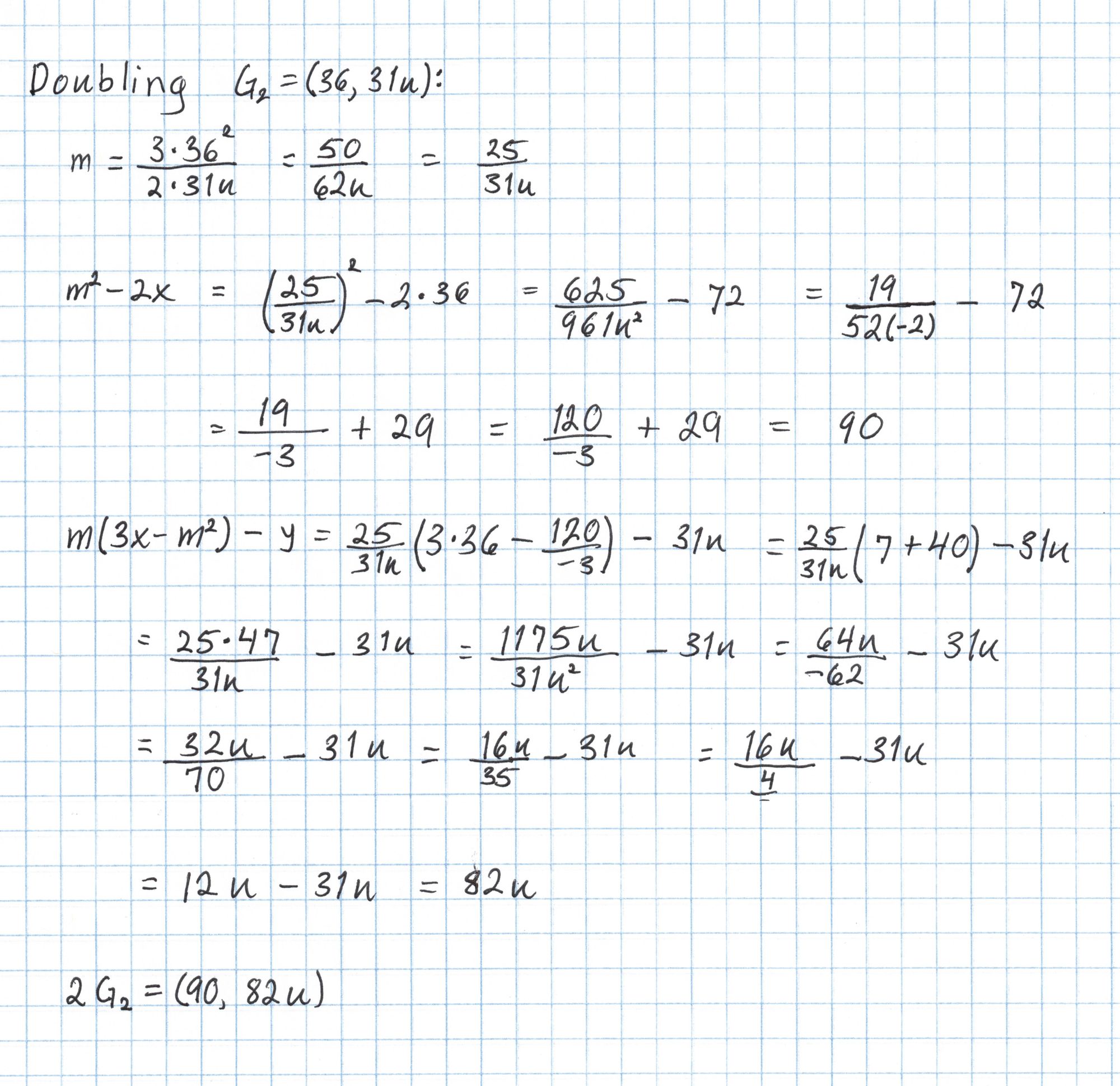
In general the point $sG_2$ can be computed much more efficiently using twisted curve methods, but in our case a simple doubling is quicker. Putting $sG_2$ together with the rest of our points gives the complete SRS.
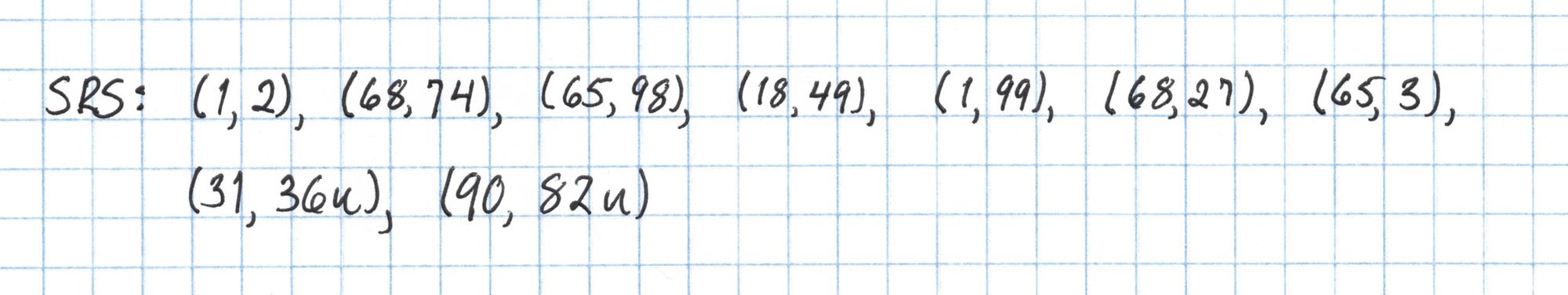
Now our setup is done! This list of elliptic curve points is the structured reference string which can be published.
Composing a PLONK-style circuit
Circuits in PLONK will end up being expressed as polynomials. The more gates there are in the circuit, the higher the degree of polynomials we may end up working with. In order to save some serious hand cramping later we will use a very small circuit.
A circuit that is pretty small but still interesting is one that tests if three numbers form a Pythagorean triple. A Pythagorean triple is three integers that could be the sides of a right triangle. The numbers $(3, 4, 5)$ form a Pythagorean triple, as do $(5, 12, 13)$ and $(9, 12, 15)$. If ordered so that the biggest number comes last, a triple $(a, b, c)$ satisfies the Pythagorean Theorem equation: $a^2 + b^2 = c^2$.
Each gate, or constraint, of a SNARK circuit is an equation that can express a limited amount of arithmetic. In both PLONK and rank-one constraint systems (R1CS) there can only be one multiplication of variables in each gate. While R1CS can do unlimited additions in a single gate, PLONK can only do one. (Two additions if you count the addition of a constant.) Since the Pythagorean Theorem equation above has three multiplications and one addition we will need four PLONK gates to express it. Here is a simplified version of the four gate equations that express the Pythagorean equation:

Composing these equations gives $x_1^2+x_3^2=x_5^2$, the Pythagorean Theorem equation we are trying to express.
Each $x_i$ variable is called a "wire". In order to satisfy the constraints we would need to supply six numbers as wire values that make all of the equations correct. For example, $\mathbf{x} = (3, 9, 4, 16, 5, 25)$ would work, as would $\mathbf{x} = (5, 25, 12, 144, 13, 169)$.
To convert these equations into PLONK gates, first notice that every equation above has a variable each on the left and right side of the operation, and then an "output" variable on the other side of the equal sign. The value in the left variable will be called $a$, in the right, $b$, and the output $c$. (These $a$, $b$, and $c$ have nothing to do with the $a$, $b$, and $c$ typically used in the Pythagorean theorem. This is just an unfortunate coincidence in variable names!)
PLONK gates have more information in them than the simplified equations above. A full PLONK gate looks like this:
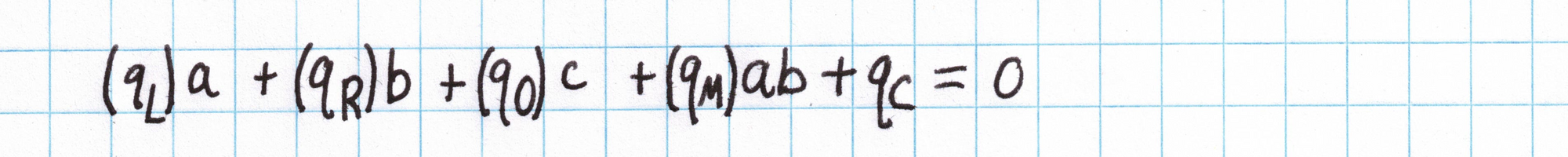
...where the $a$, $b$, and $c$ are the left, right, and output wires of the gate.
To say $a+b=c$, we let $q_L$ and $q_R$ equal 1, while $q_O$ equals -1. The other coefficients wouldn't be used, so we set $q_M$ and $q_C$ to 0.
To say $a\times b = c$, we set $q_O$ equal to -1, set $q_M$ equal 1, and set the rest of the coefficients to 0.
To bind a variable to a public value, we let $q_R$, $q_O$, $q_M$ equal to 0, $q_L$ equal to 1, and $q_C$ equal to the public value.
Considering all inputs as private, we get these four PLONK gates representing our Pythagorean circuit:
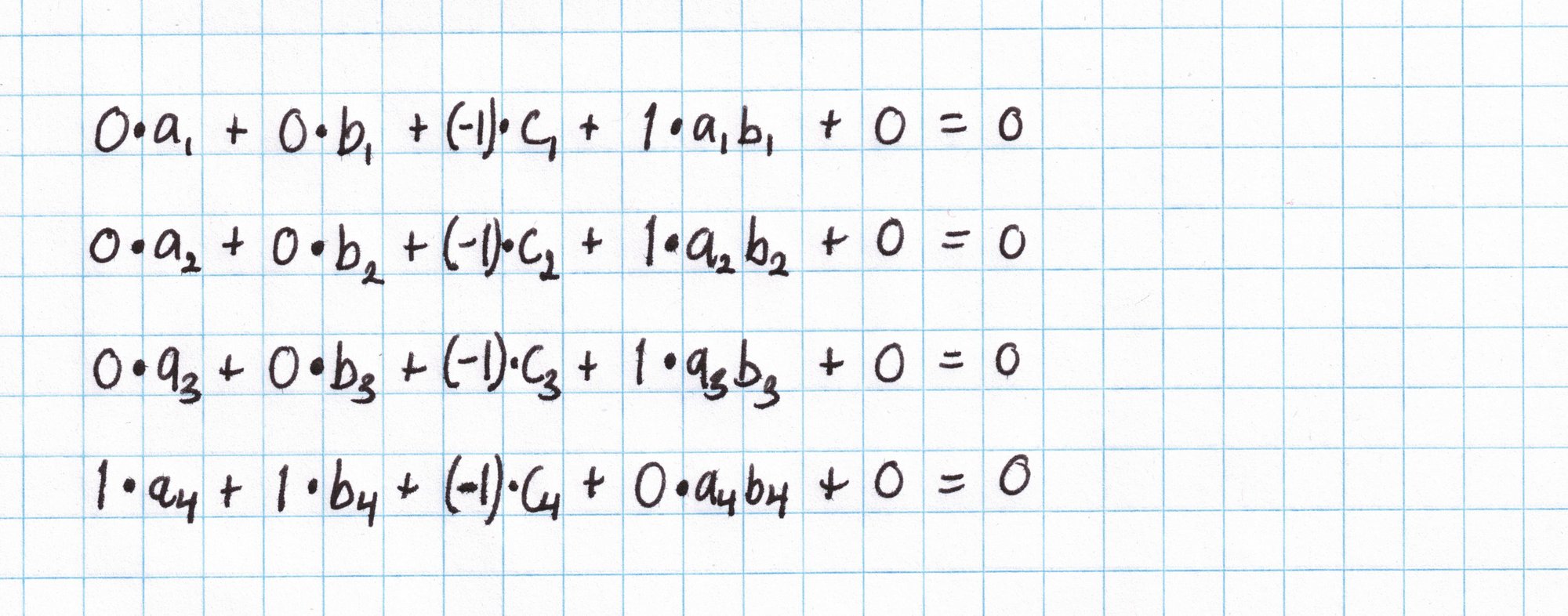
These gates say that $a_1\cdot b_1 = c_1$, $a_2\cdot b_2 = c_2$, $a_3\cdot b_3 = c_3$, and $a_4 + b_4 = c_4$. Suppose you want to use these gates to check that $(3,4,5)$ is a Pythagorean triple. The $\mathbf{a_i}$ (left) values will be $(3,4,5,9)$, the $\mathbf{b_i}$ (right) values will be $(3,4,5,16)$, and the $\mathbf{c_i}$ (out) values will be $(9, 16, 25, 25)$. Each equation should be satisfied after substituting in these values.
We collect all the $q_{L_i}$, $a_i$, and so on into vectors:
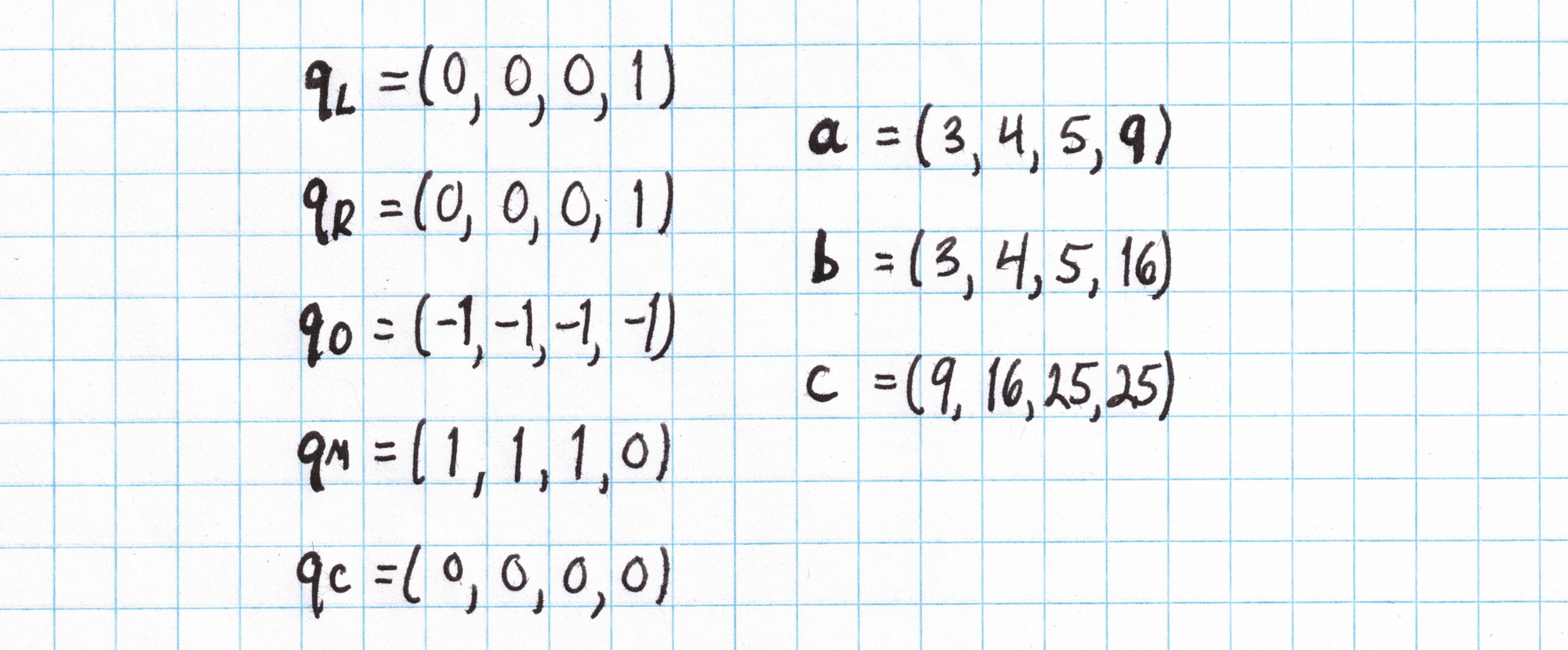
The vectors above condense all the necessary information in a nice way so we don't have to write out those full gate equations. The $\mathbf{q}$ vectors are called "selectors" and encode the structure of the circuit. The $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ vectors are "assignments" to the circuit variables and represent the Prover's private inputs.
The $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ vectors written above form an example assignment to our circuit that tests whether $(3,4,5)$ is a Pythagorean triple. We could have used assignments based on any other Pythagorean triple. (In fact certain assignments that do not represent a Pythagorean triple could satisfy this circuit! This will be taken care of in the next post when we introduce copy constraints.)
That's all we need to do to define our PLONK-style circuit. In the next post, we introduce copy constraints and will use the circuit we've made to create a proof.
Written by Joshua Fitzgerald, zero-knowledge cryptography researcher & protocol developer at Metastate.
Image credits: Koalas from Wikimedia.
Metastate has ceased its activities on the 31st of January 2021. The team members have joined a new company and working on a new project. If you're interested in zero-knowledge cryptography and cutting-edge cryptographic protocols engineering positions in Rust, check out the open positions at Heliax.
If you have any feedback or questions on this article, please do not hesitate to contact us: hello@heliax.dev.

